Nahamcon 2023: Cryptography

Intro
So maybe I haven’t written a blog post in a while, but I was able to make time for Nahamcon 2023 where my team got 35th! I managed to full solve the cryptography category, and while it wasn’t terribly difficult, there were a number of math concepts that showed up during the challenges that I thought were good enough for writeups. RSA Intro and Outro covered some RSA basics plus a little bit of algebra. Just One More was a small exercise in solving systems of linear equations. ForgeMe1 and ForgeMe2 were both related to hash length extension attacks. Finally, Signed Jeopardy was about Nintendo trivia and ECDSA nonce reuse.
RSA Intro
Description
What *is* RSA? Really Spicy Applesauce? Ridiculously Smart Alpaca? Random Squirrel Alliance? Nope, not at all. Just some dudes who made a cool public-key cryptosystem!
Author: Gary
Challenge
We’re given the output of the below source code.
from Crypto.Util.number import getStrongPrime, getPrime, bytes_to_long as b2l
FLAG = open('flag.txt', 'r').read().strip()
OUT = open('output.txt', 'w')
l = len(FLAG)
flag1, flag2, flag3 = FLAG[:l//3], FLAG[l//3:2*l//3], FLAG[2*l//3:]
# PART 1
e = 0x10001
p = getStrongPrime(1024)
q = getStrongPrime(1024)
n = p*q
ct = pow(b2l(flag1.encode()), e, n)
OUT.write(f'*** PART 1 ***\ne: {e}\np: {p}\nq: {q}\nct: {ct}')
# PART 2
e = 3
p = getStrongPrime(1024)
q = getStrongPrime(1024)
n = p*q
ct = pow(b2l(flag2.encode()), e, n)
OUT.write(f'\n\n*** PART 2 ***\ne: {e}\nn: {n}\nct: {ct}')
# PART 3
e = 65537
p = getPrime(24)
q = getPrime(24)
n = p*q
fl = round(len(flag3)/4)
f3_parts = [flag3[i:i+4] for i in range(0, len(flag3), 4)]
assert ''.join(f3_parts) == flag3
ct_parts = []
for part in f3_parts:
pt = b2l(part.encode())
assert pt < n
ct = pow(pt, e, n)
ct_parts.append(ct)
OUT.write(f'\n\n*** PART 3 ***\ne: {e}\nn: {n}\nct: {ct_parts}')
Usually, when an RSA challenge is structured like this, the parts are usually related by some common relations or variables. However, in this case, we’re basically given three distinct RSA challenge, all of which are classic examples of the misuse of RSA.
- In part 1, we encrypt the message in the normal RSA procedure, but instead of giving the normal public key of \((e,n)\), they give us \(p\) and \(q\), which is a big no no. Knowing the factors that make up the modulus lets us just make the private key.
- In part 2, we encrypt the message with an exponent of \(3\). This is not immediately a horrible thing, but the size of the message is also fairly small, and the size of the modulus is way bigger, which is why we can solve this.
- In part 3, we break up the last third of the flag into even smaller pieces and encrypt with a small modulus. On paper, nothing is immediately insecure here, but the actual modulus is so small that a computer can just factor it instantly.
There is not much left to discuss here, this challenge was rated “easy” for good reason.
Solution
As mentioned earlier, for part 1, we can directly compute the private key. To calculate it, we need to solve the below congruence for \(d\):
\[\begin{align*} & ed \equiv 1 \pmod{\phi(n)} \end{align*}\]
The \(\phi(n)\) is actually Euler’s Totient Function, which computes the number of integers less than \(n\) that are coprime to \(n\). If we know that it’s a product of two primes, we can simply compute \(\phi(n) = (p-1)(q-1)\). From there, we can let the Python take over and compute the private key and do the decryption (\(m \equiv c^d\pmod{n}\)).
from Crypto.Util.number import long_to_bytes
# part 1
e1 = 65537
p1 = # big prime
q1 = # big prime
ct1 = # big int
phi1 = (p1 - 1)*(q1 - 1)
d1 = pow(e1, -1, phi1)
flag1 = long_to_bytes(pow(ct1, d1, p1*q1))
For part 2, we don’t have the factors. However, we’re only cubing the input, which is significantly smaller than a 2048-bit modulus. The whole point of using the modulo operation in cryptography is that the inputs wrap around and become hard to traceback. A small exponent means we don’t even wrap around the modulus to begin with.
from gmpy2 import iroot
e2 = 3
n2 = # big int
ct2 = # big int
flag2 = long_to_bytes(iroot(ct2, 3)[0])
For the final part, the modulus is only ~48 bits long, which really isn’t that large as far as computers go. For context, the current standard for RSA is to use a 2048-bit, or even a 4096-bit modulus if necessary. We could be extra and use fancy math to factor the number for us, or we could just use good ol’ factordb and get the needed numbers.
# part 3: http://factordb.com/index.php?query=107710970774233
p3, q3 = 8885719, 12121807
phi3 = (p3 - 1) * (q3 - 1)
d3 = pow(e3, -1, phi3)
flag3 = b''
for ct in ct3:
flag3 += long_to_bytes(pow(ct, d3, n3))
All together, our final script looks like this:
from Crypto.Util.number import long_to_bytes, bytes_to_long
from gmpy2 import iroot
# part 1
e1 = 65537
p1 = 152933908726088000025981821717328900253841375038873501148415965946834656401640031351528841350980891403699057384028031438869081577476655254545307973436745130347696405243778481262922512227444915738801835842194123487258255790292004204412236314558718035967575479232723997430178018130995420315759809636522091902529
q1 = 173403581892981708663967289381727914513043623656015065332774927693090954681172215632003125824638611519248812013286298011144213434368768979531792528759533473573346156338400142951284462417074992959330154930806611253683603690442142765076944118447174491399811297223146324861971722035746276165056022562961558299229
ct1 = 24900222896050719055946861973957246283663114493271057619080357155524140641110166671081924849912377863714741017586072836978357770860853088772671413685690588862677870057778743649753806625109141461870634890427341765490174013453580041222600439459744928592280825572907034701116518706347830413085865254963646096687533779205345001529893651672061316525244476464884343232361498032095529980932018530224029715267731845742371944443150142380656402289372470902457020777826323051802030062577945893807552316343833971210833255536637260838474638607847822451324479398241526919184038034180388382949827367896808363560947298749154349868503
phi1 = (p1 - 1)*(q1 - 1)
d1 = pow(e1, -1, phi1)
flag1 = long_to_bytes(pow(ct1, d1, p1*q1))
e2 = 3
n2 = 17832697294201997154036617011957221780954165482288666773904510458098283881743910060438108775052144170769164876758249100567442926826366952851643073820832317493086415304740069439166953466125367940677570548218324219386987869433677168670642103353927101790341856159406926994785020050276564014860180970395749578442970075496442876475883003906961049702649859496118324912885388643549649071478725024867410660900848046927547400320456993982744075508818567475254504481562096763749301743619222457897353143558783627148704136084952125284873914605708215421331001883445600583624655438154001230490220705092656548338632165583188199066759
ct2 = 55717486909410107003108426413232346564412491530111436942121941739686926249314710854996834619
flag2 = long_to_bytes(iroot(ct2, 3)[0])
e3 = 65537
n3 = 107710970774233
ct3 = [18128889449669, 12202311999558, 10705744036504, 23864757944740]
# part 3: http://factordb.com/index.php?query=107710970774233
p3, q3 = 8885719, 12121807
phi3 = (p3 - 1) * (q3 - 1)
d3 = pow(e3, -1, phi3)
flag3 = b''
for ct in ct3:
flag3 += long_to_bytes(pow(ct, d3, n3))
print(flag1 + flag2 + flag3)
flag: flag{361862d054e2a9abe41cc315517cfa31}
RSA Outro
Description
I didn't feel like fitting this one in the RSA Intro, so here is an RSA Outro!
Author: Gary
Challenge
We’re given the output to the below code.
from Crypto.Util.number import getStrongPrime, isPrime, inverse, bytes_to_long as b2l
FLAG = open('flag.txt', 'r').read()
# safe primes are cool
# https://en.wikipedia.org/wiki/Safe_and_Sophie_Germain_primes
while True:
q = getStrongPrime(512)
p = 2*q + 1
if (isPrime(p)):
break
n = p*q
phi = (p-1)*(q-1)
e = 0x10001
d = inverse(e, phi)
pt = b2l(FLAG.encode())
ct = pow(pt,e,n)
open('output.txt', 'w').write(f'e: {e}\nd: {d}\nphi: {phi}\nct: {ct}')
Solution
This challenge is a pretty standard use of RSA, the key difference being the relationship between \(p\) and \(q\). The link in the source code has some good background knowledge, but we don’t really need to know it to solve the challenge. Here, we generate random 512-bit primes and only stop generating when \(p = 2q + 1\). In secure implementations of RSA, you do not want your primes to have some algebraic relation, because it’s divulging unnecessary information. In this case, recall that \(\phi(n) = (p-1)(q-1)\). Knowing a relationship between \(p\) and \(q\), we can actually construct an equation to solve for \(q\).
\[\begin{align*} \phi(n) &= (p-1)(q-1) \\ \phi(n) &= pq - p - q + 1 \\ \phi(n) &= (2q+1)q - (2q+1) - q + 1 \\ 0 &= 2q(q-1)-\phi(n)\end{align*}\]
We can solve this equation either using the quadratic formula, or by using a library like sympy to solve this symbolic equation. Once we’ve recovered \(q\), finding the other numbers follows a similar pattern to what we discussed in the previous challenge.
from Crypto.Util.number import long_to_bytes, bytes_to_long
from sympy import *
e = 65537
d = 53644719720574049009405552166157712944703190065471668628844223840961631946450717730498953967365343322420070536512779060129496885996597242719829361747640511749156693869638229201455287585480904214599266368010822834345022164868996387818675879350434513617616365498180046935518686332875915988354222223353414730233
phi = 245339427517603729932268783832064063730426585298033269150632512063161372845397117090279828761983426749577401448111514393838579024253942323526130975635388431158721719897730678798030368631518633601688214930936866440646874921076023466048329456035549666361320568433651481926942648024960844810102628182268858421164
ct = 37908069537874314556326131798861989913414869945406191262746923693553489353829208006823679167741985280446948193850665708841487091787325154392435232998215464094465135529738800788684510714606323301203342805866556727186659736657602065547151371338616322720609504154245460113520462221800784939992576122714196812534
var('q')
solutions = solve(2*q*(q-1)-phi, q)
q = solutions[1]
p = 2*q + 1
assert phi == (q-1)*(p-1)
m = long_to_bytes(pow(ct, d, int(p*q)))
print(m)
flag: flag{8b76b85e7f450c39502e71c215f6f1fe}
Just One More
Description
Just one more?
Author: Gary
Challenge
Once again, a static challenge.
import random
OUT = open('output.txt', 'w')
FLAG = open('flag.txt', 'r').read().strip()
N = 64
l = len(FLAG)
arr = [random.randint(1,pow(2, N)) for _ in range(l)]
OUT.write(f'{arr}\n')
s_arr = []
for i in range(len(FLAG) - 1):
s_i = sum([arr[j]*ord(FLAG[j]) for j in range(l)])
s_arr.append(s_i)
arr = [arr[-1]] + arr[:-1]
OUT.write(f'{s_arr}\n')
When I solve cryptography challenges, one thing that helps me is translating source code to actual math, so it’s easier to process. Here, we’re generating a list of random numbers as long as the flag, and generating various sums. The corresponding indices of the random numbers and the flag are multiplied together, and then added. Afterwards, the list of random numbers is rotated to the right by one.
Let’s call each element of arr \(r_i\), each character of the flag \(f_i\), and each resulting sum as \(s_i\),
where \(i\) is the index. We can then rewrite what this code is generating:
\[\begin{align*} r_1f_1 + r_2f_2 + r_3f_3 + … + r_{38}f_{38} &= s_1 \\ r_{38}f_1 + r_1f_2 + r_2f_3 + … + r_{37}f_{38} &= s_2 \\ r_{37}f_1 + r_{38}f_2 + r_1f_3 + … + r_{36}f_{38} &= s_3 \\ & \vdots \\ r_3f_1 + r_4f_2 + r_5f_3 + … + r_2f_{38} &= s_{37} \\ \end{align*}\]
What this is, now, is not some weird for loop, but just a system of linear equations, which we can actually solve.
Solution
If you’ve only ever taken an algebra or even a calculus course, systems with more than three equations can seem daunting. However, when you study Linear Algebra, finding solutions can feel almost trivial when you have computers. Knowing the random numbers, we can treat those as coefficients, and rewrite this system as a matrix:
\[\begin{bmatrix} r_1 & r_2 & r_3 & … & r_{38} & s_1 \\ r_{38} & r_1 & r_2 & … & r_{37} & s_2 \\ r_{37} & r_{38} & r_1 & … & r_{36} & s_3 \\ \vdots & \vdots & \vdots & … & \vdots & \vdots \\ r_3 & r_4 & r_5 & … & r_2 & s_{37} \end{bmatrix}\]
Each column represents a variable, in this case, the unknown values of our flag. From here, we want to transform the matrix into what’s known as reduced row echelon form (RREF) without changing the solution of the system, because that form (ideally) has 1’s along the diagonal and zeroes everywhere else. This means whatever is in the rightmost columns would be the solution to our system.
The primary way we can take a matrix and put it into RREF is through Gaussian Elimination, where we only use elementary row operations (i.e. things that don’t change the solution to the system) to slowly work our way to RREF. This could be swapping rows, rescaling a row, or adding rows, all of which preserve the original solutions. This explanation is a little bit of an oversimplification, so reading some of the hyperlinks here might give a fuller explanation.
Regardless, we’re not in math class, and we can do this pretty quickly with computers. Using SageMath, I can build a matrix like we described, and use the Matrix.rref() function to do all of this computation for us.
from sage.all import *
arr = # array
flag_enc = # array
tmp = arr
mat = []
for i in range(37):
mat.append(tmp + [flag_enc[i]])
tmp = [tmp[-1]] + tmp[:-1]
eqns = matrix(mat)
ref = eqns.rref()
However, if we check the last column of this matrix, we see that the numbers are a bit bigger than what the flag should be (output omitted because it’s a lot). Doing some further investigation, it appears our matrix was reduced to something along the lines of:
\[\begin{bmatrix} 1 & 0 & 0 & … & k_1 & s’_1 \\ 0 & 1 & 0 & … & k_2 & s’_2 \\ 0 & 0 & 1 & … & k_3 & s’_3 \\ \vdots & \vdots & \vdots & … & \vdots & \vdots \\ 0 & 0 & 0 & … & s’_{37} & s_{37} \end{bmatrix}\]
(Note that I’m using new variables since the values are different from the original matrix)
The reason that the reduced matrix isn’t as “clean” is because in the original challenge, we only made 37 sums, instead of 38. If we had all 38, this challenge would be over instantly. However, if we rewrite this matrix as a list of equations again, we see that they’re all in the form \(f_i + k_if_{38} = s'_i\). However, we know the flag format already, and that the last character is just ‘}’. Knowing this, we can just take the last column, minus the column of k’s times the ASCII code for ‘}’, and fully recover the flag.
from sage.all import *
arr = [12407953253235233563, 3098214620796127593, 18025934049184131586, 14516706192923330501, 13439587873423175563, 17668371729629097289, 4983820371965098250, 1941436363223653079, 15491407246309500298, 8746935775477023498, 911995915798699052, 16286652540519392376, 13788248038504935294, 18140313902119960073, 11357802109616441330, 2498891881524249135, 9088680937359588259, 14593377776851675952, 2870989617629497346, 18249696351449250369, 2029516247978285970, 14734352605587851872, 8485311572815839186, 8263508188473851570, 14727305307661336083, 6229129263537323513, 17136745747103828990, 8565837800438907855, 17019788193812566822, 9527005534132814755, 1469762980661997658, 16549643443520875622, 9455193414123931504, 12209676511763563786, 271051473986116907, 17058641684143308429, 13420564135579638218, 7599871345247004229]
flag_enc = [35605255015866358705679, 36416918378456831329741, 35315503903088182809184, 36652502430423040656502, 34898639998194794079275, 36303059177758553252637, 35047128751853183340357, 36513205019421922844286, 35188395228735536982649, 35301216188296520201752, 35877364908848326577377, 35548407875093684038138, 36846989992339836295226, 35424096673112978582599, 35435941095923989701820, 35884660233631412675912, 35250569480372437220096, 36071512852625372107309, 35636049634203159168488, 35407704890518035619865, 35691117250745693469087, 35942285968400856168658, 35659245396595333737528, 34682110547383898878610, 36251061019324605768432, 34350337346574061914637, 36706069443188806905153, 35296365364968284652906, 34767397368306249667499, 37665777691001951216694, 33927027243025444519647, 37464577169642287783563, 34818703279589326375333, 35526731706613463585509, 36698165076109278070662, 34612009622491263626134, 37224659068886403545747]
tmp = arr
mat = []
for i in range(37):
mat.append(tmp + [flag_enc[i]])
tmp = [tmp[-1]] + tmp[:-1]
eqns = matrix(mat)
ref = eqns.rref()
print(bytearray(list(ref.columns()[-1] - (ord('}')*ref.columns()[-2]))).decode() + '}')
flag: flag{aad9ba9b3fdfa4cc6f7e2e18d0dcbbab}
ForgeMe 1 and 2
Description
ForgeMe1: Can you break my hashed-based MAC? Below are some resources that may be useful.
ForgeMe2: Can you break my hashed-based MAC again? Below are some resources that may be useful.
Author: Gary
Challenge
These were technically two separate challenges, but ForgeMe1 was just an easier version of ForgeMe2, so I’ll only be talking about ForgeMe2, and you can probably figure out ForgeMe1 instantly. Both challenges were dynamic, so below is the server code for ForgeMe2.
import socket
import threading
from _thread import *
from Crypto.Random import get_random_bytes, random
from binascii import hexlify, unhexlify
import crypto
from wonderwords import RandomWord
HOST = '0.0.0.0' # Standard loopback interface address (localhost)
PORT = 1234 # Port to listen on (non-privileged ports are > 1023)
FLAG = open('flag.txt', 'r').read().strip()
MENU = "\nWhat would you like to do?\n\t(1) MAC Query\n\t(2) Verification Query\n\t(3) Forgery\n\t(4) Exit\n\nChoice: "
INITIAL = "Can you break my hashed-based MAC again?\n"
MAX_QUERIES = 100
TAGLEN = 20 # SHA1() tag is 20 bytes
INJECTION = b'https://www.youtube.com/@_JohnHammond'
# t = H(key || msg)
def hashed_mac(msg, key):
h = crypto.Sha1(key + msg)
t = h.hexdigest()
return t
# H(key || msg) == tag
def vf_query(conn, key, first_part=None):
conn.sendall(b'msg (hex): ')
msg = conn.recv(1024).strip()
conn.sendall(b'tag (hex): ')
tag = conn.recv(1024).strip()
try:
msg = unhexlify(msg)
if first_part is not None and (first_part not in msg or INJECTION not in msg):
conn.sendall(f'forgot something!\n'.encode())
elif len(tag) != TAGLEN*2:
conn.sendall(f'Invalid tag length. Must be {TAGLEN} bytes\n'.encode())
else:
t_ret = hashed_mac(msg, key)
return t_ret.encode() == tag, msg
except Exception as e:
conn.sendall(b'Invalid msg format. Must be in hexadecimal\n')
return False, b''
def mac_query(conn, key):
conn.sendall(b'msg (hex): ')
msg = conn.recv(1024).strip()
try:
msg = unhexlify(msg)
t = hashed_mac(msg, key)
conn.sendall(f'H(key || msg): {t}\n'.encode())
return msg
except Exception as e:
conn.sendall(b'Invalid msg format. Must be in hexadecimal\n')
return None
def threading(conn):
conn.sendall(INITIAL.encode())
rw = RandomWord()
first_part = '-'.join(rw.random_words(random.randrange(5,30), word_min_length=5)).encode()
conn.sendall(f'first_part: {first_part.decode()}\n'.encode())
key = get_random_bytes(random.randrange(10,120))
queries = []
while len(queries) < MAX_QUERIES:
conn.sendall(MENU.encode())
try:
choice = conn.recv(1024).decode().strip()
except ConnectionResetError as cre:
return
# MAC QUERY
if choice == '1':
msg = mac_query(conn, key)
if msg is not None:
queries.append(msg)
# VF QUERY
elif choice == '2':
res, msg = vf_query(conn, key)
conn.sendall(str(res).encode())
# FORGERY
elif choice == '3':
res, msg = vf_query(conn, key, first_part)
if res and msg not in queries:
conn.sendall(FLAG.encode() + b'\n')
elif msg in queries:
conn.sendall(b"cheater!!!\n")
else:
conn.sendall(str(res).encode() + b'\n')
break
# EXIT or INVALID CHOICE
else:
if choice == '4':
conn.sendall(b'bye\n')
else:
conn.sendall(b'invalid menu choice\n')
break
if len(queries) > MAX_QUERIES:
conn.sendall(f'too many queries: {len(queries)}\n'.encode())
conn.close()
if __name__ == "__main__":
with socket.socket(socket.AF_INET, socket.SOCK_STREAM) as s:
s.setsockopt(socket.SOL_SOCKET, socket.SO_REUSEADDR, 1)
s.bind((HOST, PORT))
s.listen()
while True:
conn, addr = s.accept()
print(f'new connection: {addr}')
start_new_thread(threading, (conn, ))
s.close()
In cryptography, a Message Authentication Code (MAC) is a construction that uses a secret key to enable checking the authenticity of a message, that is typically associated with symmetric encryption schemes. The output of a MAC, called a tag, is sent with the message. The recipient will then compute the tag themselves, and if the received tag does not match the computed tag, the message is rejected as forgery.
This server is a MAC oracle with 2 main functions:
- Option 1 lets us input a message, and the server will output a tag. In particular, our tag is the output of \(\texttt{SHA-1}(K \vert \vert m)\), where \(K\) is a key of random length from 10 to 120 bytes.
- Option 2 lets us input a tag and a message, and the server will tell us whether or not that combination of message and tag is valid. That message must contain a phrase generated by the server, and the link to John Hammond’s YouTube challenge.
The third option on the server is the goal of the challenge. Upon connecting to the server, we’re given a random phrase, and we’re supposed to forge a tag that start contains the random phrase, and the link to John Hammond’s channel. This would be as easy as asking the oracle for the tag and then just giving it back, but the server keeps track of our queries, so we cannot give it a message and reuse that tag for getting the flag.
Solution
The key to this challenge is that the MAC construction is fundamentally flawed with its choice of hash function. Although SHA1 has long been considered insecure due to the discovery of multiple collisions, the issue lies in iterative hash functions. SHA-1 is based on the Merkle–Damgård construction, which will break up a message into blocks, apply the compression function to the first block, and then uses the result of that in computing the compression function of the next block, until we’ve gotten through the whole message and produced an output digest. Below is a diagram of this:
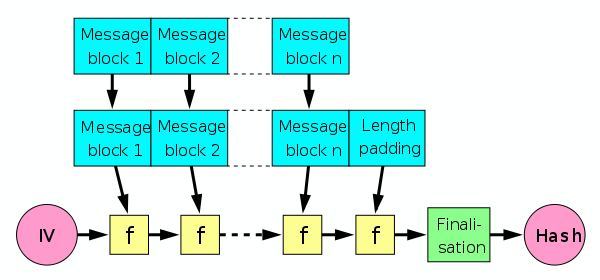 Courtesy: Wikipedia
Courtesy: Wikipedia
(If this hash talk has you confused, here’s a link on Wikipedia to catch you up to speed: link)
The internals of SHA-1 beyond this are relatively unimportant, what matters is that the output hash is just whatever the internal state of the hash was whenever we ran out of message/padding to use. This is where the hash length extension attack originates. We can treat the hash/tag as our new starting state, append some stuff to the message that was hashed, and run the function from there. Recall that MAC was computed by doing \(\texttt{SHA-1}(K \vert\vert m)\). Using the hash length extension attack, we can take this result and forge a tag for \(\texttt{SHA-1}(K \vert\vert m \vert\vert m')\), where \(m'\) is a message that we add.
Normally, writing this yourself is a fun exercise and really helps you understand the concepts. However, iagox86 has already written a pretty solid tool called hash_extender to do most of the heavy lifting for us. As of writing, there’s a weird error in the Makefile having to do with OpenSSL 3.0, but this fork from Michele0303 fixes it. I’ll clone the repository to my machine, and use make to build the program.
an00b@capacitor:~/dev/ctf/CTF/live_events/nahamcon_23$ git clone https://github.com/Michele0303/hash_extender.git
Cloning into 'hash_extender'...
remote: Enumerating objects: 647, done.
remote: Counting objects: 100% (23/23), done.
remote: Compressing objects: 100% (18/18), done.
remote: Total 647 (delta 7), reused 11 (delta 5), pack-reused 624
Receiving objects: 100% (647/647), 190.32 KiB | 1.49 MiB/s, done.
Resolving deltas: 100% (424/424), done.
nayr@capacitor:~/dev/ctf/CTF/live_events/nahamcon_23$ cd hash_extender/
nayr@capacitor:~/dev/ctf/CTF/live_events/nahamcon_23/hash_extender$ make
[CC] buffer.o
[CC] formats.o
[CC] hash_extender.o
[CC] hash_extender_engine.o
[CC] test.o
[CC] tiger.o
[CC] util.o
[LD] hash_extender
[CC] hash_extender_test.o
[LD] hash_extender_test
an00b@capacitor:~/dev/ctf/CTF/live_events/nahamcon_23/hash_extender$ ./hash_extender --help
--------------------------------------------------------------------------------
HASH EXTENDER
--------------------------------------------------------------------------------
By Ron Bowes <ron @ skullsecurity.net>
See LICENSE.txt for license information.
Usage: ./hash_extender <--data=<data>|--file=<file>> --signature=<signature> --format=<format> [options]
At this point, ForgeMe1 has been solved. You just use this tool to forge a hash. In ForgeMe2, however, we have a problem where we don’t know the size of the key that’s been prepended. If we don’t know the size, we can’t accurately compute the padding needed to forge the tag. Luckily, the server gives us 100 queries, so we can just brute force the size of the key until the server returns true, and once we know that size, we can submit a correctly forged tag to get the flag.
from pwn import *
import subprocess
context.log_level == 'debug'
def start(argv=[], *a, **kw):
if args.REMOTE: # ('server', 'port')
return remote(sys.argv[1], sys.argv[2], *a, **kw)
else: # Run locally
return error("Need to specify args!!!")
INJECT = 'https://www.youtube.com/@_JohnHammond'
io = start()
io.recvuntil('first_part:')
first_part = io.recvlineS().strip()
io.sendlineafter('Choice:', '1')
io.sendlineafter('msg (hex):', first_part.encode().hex())
io.recvuntil('H(key || msg):')
tag = io.recvlineS().strip()
info(f"First part: {first_part}")
info(f"Tag: {tag}")
secret_len = None
for i in range(10,120):
result = subprocess.run(['../hash_extender/hash_extender', '--data', first_part, '--secret', str(i), '--append', f"'{INJECT}'", '--signature', tag, '--format', 'sha1'], stdout=subprocess.PIPE).stdout
sections = result.decode().split('\n')
forged_tag = sections[2].split(':')[1].strip()
forged_string = sections[3].split(':')[1].strip()
#info(f"Forged tag: {forged_tag}")
#info(f"Forged string: {forged_string}")
io.sendlineafter('Choice:', '2')
io.sendlineafter('msg (hex):', forged_string)
io.sendlineafter('tag (hex):', forged_tag)
if io.recvlineS().strip() == 'True':
secret_len = i
info(f"Secret len: {secret_len}")
break
if secret_len is None:
error("failure :(")
io.sendlineafter('Choice:', '3')
io.sendlineafter('msg (hex):', forged_string)
io.sendlineafter('tag (hex):', forged_tag)
flag = io.recvlineS()
success(flag)
flag (forgeme1): flag{4179e0a0f6ddc273a8a18440c979bbb7}
flag (forgeme2): flag{257843b6ca2a7678857f9caf21dd92f0}
Signed Jeopardy
Description
Let's play a special form of Jeopardy involving ECDSA!
Author: awesome10billion
Challenge
This one was also a dynamic challenge, this time written in SageMath.
from random import randint
from hashlib import sha512
with open("flag.txt",'r') as f:
flag = f.read()
questions = []
answers = []
with open('questions.txt','r') as f:
for x in f.readlines():
a = x.split('\t')
questions.append(a[0])
answers.append(a[1][:-1])
# P521 standard curve parameters
p = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
a = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057148
b = 1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
Gx = 2661740802050217063228768716723360960729859168756973147706671368418802944996427808491545080627771902352094241225065558662157113545570916814161637315895999846
Gy = 3757180025770020463545507224491183603594455134769762486694567779615544477440556316691234405012945539562144444537289428522585666729196580810124344277578376784
E = EllipticCurve(GF(p), [a, b])
G = E(Gx, Gy)
n = 6864797660130609714981900799081393217269435300143305409394463459185543183397655394245057746333217197532963996371363321113864768612440380340372808892707005449
k = randint(1,n-1)
d = randint(1,n-1)
Pub = d*G
def menu():
print("\nWhat service would you like?")
print("\t1. Question")
print("\t2. Flag")
print("\t3. Quit")
def sign():
index = randint(0,len(questions)-1)
question = questions[index]
answer = "What is "+answers[index].upper()+"?"
m_hash = int(sha512(answer.encode()).hexdigest(), 16)
P = k*G
r = int(P[0]) % n
s = ((m_hash + (r*d))/k)%n
print(f"Here is the question: {question}\nAnd here is the signature: ({r}, {s})")
def get_flag():
print("Please give the message")
message = input("")
for a in answers:
if a.casefold() in message.casefold():
print("I can't have you using the answer of one of the questions as the message!")
quit()
print("Please give the r value of the signature")
r_given = int(input(""))
print("Please give the s value of the signature")
s_given = int(input(""))
m_hash = int(sha512(message.encode()).hexdigest(), 16)
P = k*G
r = int(P[0]) % n
s = ((m_hash + (r*d))/k)%n
if r == r_given and s == s_given:
print(f"As promised, here's your flag --> {flag}")
quit()
else:
print("Not the right signature. HAHAHA!")
def main():
print(f"Welcome to my ECDSA Jeopardy!\nHere is the public key:\nPublic key = {Pub}\nI'll sign the answers and give them to you.")
while True:
menu()
choice = int(input(""))
if choice == 1:
sign()
elif choice == 2:
get_flag()
elif choice == 3:
quit()
else:
print("Invalid choice. Please try again.")
if __name__ == "__main__":
main()
Similar to the previous challenge, the goal here is signature forgery. In this case, we are asked questions about Nintendo and their associated franchises, and we’re only given the signature of the answer. We’re allowed as many questions as we want, but ultimately, we need to forge any message to get the flag.
Solution
We’ve talked about elliptic curves here before, but not necessarily using them to sign messaged. The Elliptic Curve Digital Signature Algorithm (ECDSA) is a variant of the Digital Signature Algorithm that uses elliptic curves, much like how elliptic curve Diffie-Hellman is a variant on the original Diffie-Hellman algorithm. The algorithm is described below:
- Calculate a hash of a message, call it \(h = \texttt{hash}(m)\)
- Randomly pick a nonce (\(k\)) , in this case, a number from \(1\) to \(n-1\), where \(n\) is the order of the curve
- The first part of the signature, \(r\) is computed as the x-coordinate of the point \(k*G\), where \(G\) is the generator point on the curve
- The signature is computed as \(s = k^{-1}(h+rd) \pmod{n}\), where \(d\) is the private key. The resulting signature is \((r,s)\).
This, assuming the curve is secure, is a very secure way of signing messages. However, as with all CTF challenges, there’s a fatal flaw with the implementation we have in this challenge. A nonce is a “Number used once” is meant to “seed” our algorithm, and can absolutely be made public, but should only ever be used once. The server in this case is reusing a nonce, and knowing that, it only takes two valid signatures to completely reverse the private key, which will let us sign arbitrary messages.
We can find the nonce like so: \[\begin{align*} s_1 - s_2 &= k^{-1}(h_1 + r_1d) - k^{-1}(h_2 + r_2d) \\ s_1 - s_2 &= k^{-1}(h_1 - h_2 + d(r_1 - r_2))\\ s_1 - s_2 &= k^{-1}(h_1 - h_2) \\ k &= (h_1 - h_2)(s_1-s_2)^{-1} \end{align*}\]
The \(d(r_1-r_2)\) disappears because we know \(k\) is constant, so \(R = kG\) will always be the same thing, making \(r_1 - r_2 = 0\). Once we know the nonce, we can then find the private key by rearranging the equation for \(s\) to be equivalent to \(d\).
\[\begin{align*} s &= k^{-1}(h + rd) \\ ks &= h + rd \\ d &= (ks - h)r^{-1} \end{align*}\]
A bit of jumping around with that work, we’re just moving variables back and forth until we’ve isolated \(d\). The only challenge, then, is to make sure we’re getting the trivia right so we know what the message is. Luckily, the server gives us the public key, which we can use to verify our solutions, which I put in my script (because the difference between “SEATTLE MARINERS” and “THE SEATTLE MARINERS” killed me for at least an hour). I did steal the actual attack implementation from jvdsn, but that was more for speed and I was a bit lazy.
from pwn import *
from math import gcd
from hashlib import sha512
from sage.all import *
context.log_level = 'debug'
# Allows you to switch between local/GDB/remote from terminal
def start(argv=[], *a, **kw):
if args.REMOTE: # ('server', 'port')
return remote(sys.argv[1], sys.argv[2], *a, **kw)
else: # Run locally
return exit() #process([exe] + argv, *a, **kw)
# taken from https://github.com/jvdsn/crypto-attacks/blob/master/attacks/ecc/ecdsa_nonce_reuse.py
def solve_congruence(a, b, m):
"""
Solves a congruence of the form ax = b mod m.
:param a: the parameter a
:param b: the parameter b
:param m: the modulus m
:return: a generator generating solutions for x
"""
g = gcd(a, m)
a //= g
b //= g
n = m // g
for i in range(g):
yield (pow(a, -1, n) * b + i * n) % m
def attack(n, m1, r1, s1, m2, r2, s2):
"""
Recovers the nonce and private key from two messages signed using the same nonce.
:param n: the order of the elliptic curve
:param m1: the first message
:param r1: the signature of the first message
:param s1: the signature of the first message
:param m2: the second message
:param r2: the signature of the second message
:param s2: the signature of the second message
:return: generates tuples containing the possible nonce and private key
"""
for k in solve_congruence(int(s1 - s2), int(m1 - m2), int(n)):
for x in solve_congruence(int(r1), int(((k * s1)%int(n)) - m1), int(n)):
yield int(k), int(x)
def verify_sig(m, sig, n, G, pubkey):
s1 = pow(sig[1], -1, n)
R = (m * s1) * G + (sig[0] * s1) * pubkey
#print(R)
r_prime = R[0]
return sig[0] == r_prime
p = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057151
a = 6864797660130609714981900799081393217269435300143305409394463459185543183397656052122559640661454554977296311391480858037121987999716643812574028291115057148
b = 1093849038073734274511112390766805569936207598951683748994586394495953116150735016013708737573759623248592132296706313309438452531591012912142327488478985984
Gx = 2661740802050217063228768716723360960729859168756973147706671368418802944996427808491545080627771902352094241225065558662157113545570916814161637315895999846
Gy = 3757180025770020463545507224491183603594455134769762486694567779615544477440556316691234405012945539562144444537289428522585666729196580810124344277578376784
n = 6864797660130609714981900799081393217269435300143305409394463459185543183397655394245057746333217197532963996371363321113864768612440380340372808892707005449
E = EllipticCurve(GF(p), [a, b])
G = E(Gx, Gy)
io = start()
io.recvlineS()
io.recvlineS()
# NOTE: for some reason the io.recvlineS() was getting cut off so I couldn't grab the whole public key, so you'll have to input it manually (too lazy to use regex :P)
#pubkey = io.recvlineS() + io.recvlineS()
#print(pubkey)
#dGx, dGy = [int(x.strip()) for x in pubkey[14:-1].split(':')][:-1]
#print((dGx, dGy))
dGx = int(input('dGx> '))
dGy = int(input('dGy> '))
pub_pt = E(dGx, dGy)
#exit()
io.sendlineafter('3. Quit', '1')
info(f"Quebbin 1: {io.recvlineS()}")
io.recvuntil('signature: ')
sig1 = eval(io.recvlineS())
is_correct = False
while not is_correct:
msg1 = "What is "+input("Answer? ").strip().upper()+"?"
info(f"Answer 1: {msg1}")
msg1 = int(sha512(msg1.encode()).hexdigest(), 16)
is_correct = verify_sig(msg1, sig1, n, G, pub_pt)
io.sendlineafter('3. Quit', '1')
info(f"Quebbin 2: {io.recvlineS()}")
io.recvuntil('signature: ')
sig2 = eval(io.recvlineS())
is_correct = False
while not is_correct:
msg2 = "What is "+input("Answer? ").strip().upper()+"?"
info(f"Answer 2: {msg2}")
msg2 = int(sha512(msg2.encode()).hexdigest(), 16)
is_correct = verify_sig(msg2, sig2, n, G, pub_pt)
info(f"Msg 1: {msg1}")
info(f"Msg 2: {msg2}")
info(f"Sig 1: {sig1}")
info(f"Sig 2: {sig2}")
sols = list(attack(n, msg1, sig1[0], sig1[1], msg2, sig2[0], sig2[1]))
k, d = sols[0]
info(f"Nonce and Private Key: {sols}")
print("=========================== TESTS ===========================")
try:
assert d*G == pub_pt
except AssertionError:
info("fail! d value is not correct")
try:
m = msg1
P = k*G
r = int(P[0]) % n
s = int(((m + (r*d))/k)%n)
assert r == sig1[0]
info("r1 is correct")
assert s == sig1[1]
info("s1 is correct")
except AssertionError:
info("fail! Failed to sign first message!")
try:
m = msg2
P = k*G
r = int(P[0]) % n
s = int(((m + (r*d))/k)%n)
assert r == sig2[0]
info("r2 is correct")
assert s == sig2[1]
info("s2 is correct")
except AssertionError:
info("fail! Failed to sign second message!")
print("=========================== TESTS ===========================")
io.sendlineafter('3. Quit', '2')
forged_msg = 'I want to just leave forever and ever'
m = int(sha512(forged_msg.encode()).hexdigest(), 16)
P = k*G
r = int(P[0]) % n
s = int(((m + (r*d))*pow(k, -1, n))%n)
info(f'Forged: {(r,s)}')
io.sendlineafter('Please give the message', forged_msg)
io.sendlineafter('Please give the r value of the signature', str(r))
io.sendlineafter('Please give the s value of the signature', str(s))
io.interactive()
flag: flag{a8168c41537604546394c13c8f4ef4b8}
Conclusion
Overall, had a fun time playing this year’s edition of Nahamcon. Honestly, the cryptography was not that hard, but I hope that for those reading, it was a good introduction to some of these attacks and using math.
Until next time!
Comments